You like quadratics? Here's 7 more

The following '7 quadratics' work was done on the morning of 5th Jan 2005 (my 59th birthday)

The seven quadratics given here are those whose prime values produce the even squares in the cubes-squares relationship, in the sense that:

Theorem . ...

> P[1,3] := proc(p) local r, k; r := 1;
for k from 2 to (p-1)/3 do
r := mods(r*k, p) od; r; end:

>

> poly0 := 108*R^2 + 1; # r = 2*R in 1+27*r^2
a0 := 108; b0 := 0; c0 := 1;
Delta0 := b0^2 - 4*a0*c0;
sqrt(Delta0);

poly0 := 108*R^2+1

a0 := 108

b0 := 0

c0 := 1

Delta0 := -432

12*I*sqrt(3)

>

I need to solve

(1) 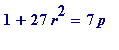1+27*r^2 = 7*p , subject to r even . So, I need R (mod 7), then r = 2W
(2) 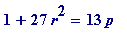1+27*r^2 = 13*p , subject to r even . So, I need R (mod 13), then r = 2W
 (3) 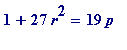1+27*r^2 = 19*p , subject to r even . So, I need R (mod 19), then r = 2W

(1) The 7 p case

> msolve(1 + 27*(2*W)^2 = 0, 7); # so W=7R+3, 4

{W = 3}, {W = 4}

Thus r is defined by r = 2W = 14R + 6 or 8

> i := 1:
poly||i := sort(expand((1+27*(14*R+6)^2)/7)); # r=14*R+6
a||i := op(1, op(1, poly||i));
b||i := op(1, op(2, poly||i));
c||i := op(1, op(3, poly||i));
Delta||i := b||i^2 - 4*a||i*c||i;
sqrt(Delta||i);

poly1 := 756*R^2+648*R+139

a1 := 756

b1 := 648

c1 := 139

Delta1 := -432

12*I*sqrt(3)

> i := 2:
poly||i := sort(expand((1+27*(14*R+8)^2)/7)); # r = 14*R+8
a||i := op(1, op(1, poly||i));
b||i := op(1, op(2, poly||i));
c||i := op(1, op(3, poly||i));
Delta||i := b||i^2 - 4*a||i*c||i;
sqrt(Delta||i);

poly2 := 756*R^2+864*R+247

a2 := 756

b2 := 864

c2 := 247

Delta2 := -432

12*I*sqrt(3)

> poly1; poly2;

756*R^2+648*R+139

756*R^2+864*R+247

>

(2) The 13 p case

> msolve(1 + 27*(2*W)^2 = 0, 13); # so W = 13R+4, 9

{W = 4}, {W = 9}

Thus r is defined by r = 2W = 26R + 8 or 18

> i := 3:
poly||i := sort(expand((1+27*(26*R+8)^2)/13)); # r = 26*R+8
factor(poly||i);
a||i := op(1, op(1, poly||i));
b||i := op(1, op(2, poly||i));
c||i := op(1, op(3, poly||i));
Delta||i := b||i^2 - 4*a||i*c||i;
sqrt(Delta||i);

poly3 := 1404*R^2+864*R+133

1404*R^2+864*R+133

a3 := 1404

b3 := 864

c3 := 133

Delta3 := -432

12*I*sqrt(3)

> i := 4:
poly||i := sort(expand((1+27*(26*R+18)^2)/13)); # r = 26R+18
a||i := op(1, op(1, poly||i));
b||i := op(1, op(2, poly||i));
c||i := op(1, op(3, poly||i));
Delta||i := b||i^2 - 4*a||i*c||i;
sqrt(Delta||i);

poly4 := 1404*R^2+1944*R+673

a4 := 1404

b4 := 1944

c4 := 673

Delta4 := -432

12*I*sqrt(3)

> poly3; poly4;

1404*R^2+864*R+133

1404*R^2+1944*R+673

>

(3) The 19 p case

> msolve(1 + 27*(2*W)^2 = 0, 19); # so W = 13R+4, 15

{W = 4}, {W = 15}

Thus r is defined by r = 2W = 38R + 8 or 30

> i := 5:
poly||i := sort(expand((1+27*(38*R+8)^2)/19)); # r = 38*R+8
a||i := op(1, op(1, poly||i));
b||i := op(1, op(2, poly||i));
c||i := op(1, op(3, poly||i));
Delta||i := b||i^2 - 4*a||i*c||i;
sqrt(Delta||i);

poly5 := 2052*R^2+864*R+91

a5 := 2052

b5 := 864

c5 := 91

Delta5 := -432

12*I*sqrt(3)

> i := 6:
poly||i := sort(expand((1+27*(38*R+30)^2)/19)); # r = 38*R+30
a||i := op(1, op(1, poly||i));
b||i := op(1, op(2, poly||i));
c||i := op(1, op(3, poly||i));
Delta||i := b||i^2 - 4*a||i*c||i;
sqrt(Delta||i);

poly6 := 2052*R^2+3240*R+1279

a6 := 2052

b6 := 3240

c6 := 1279

Delta6 := -432

12*I*sqrt(3)

> poly5; poly6;

2052*R^2+864*R+91

2052*R^2+3240*R+1279

>

> for i from 0 to 6 do [i, poly||i] od;

[0, 108*R^2+1]

[1, 756*R^2+648*R+139]

[2, 756*R^2+864*R+247]

[3, 1404*R^2+864*R+133]

[4, 1404*R^2+1944*R+673]

[5, 2052*R^2+864*R+91]

[6, 2052*R^2+3240*R+1279]

>

The primes in the first of those seven sets of primes { p } - the ones generated by 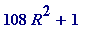108*R^2+1 - are rather special:

each has the beautiful property that P[1,3](p)^3 = (p-1)/2 (mod p )

i.e. 2*P[1,3](p)^3 = -1 (mod p )

I had observed those primes yesterday (4th Jan), but only now (5th Jan) do they make sense , in terms of having that polynomial structure to them.

In terms of the Berndt, Evans, and Williams binomial coefficients theorems in Chapter 9, those primes have the property that

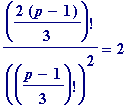(2*(p-1)/3)!/(((p-1)/3)!^2) = 2 (mod p )

> with(numtheory):

> i := 0:
for R from 0 to 30 do
if isprime(poly||i(R)) then print(poly||i(R),
(poly||i(R) - 1)/order(P[1,3](poly||i(R)), poly||i(R))) fi od;

109, 1

433, 2

3889, 2

18253, 1

21169, 14

43201, 2

47629, 1

73009, 2

84673, 24

> i := 1:
for R from 0 to 30 do
if isprime(poly||i(R)) then print(poly||i(R),
(poly||i(R) - 1)/order(P[1,3](poly||i(R)), poly||i(R))) fi od;

139, 2

1543, 2

8887, 2

14827, 42

22279, 2

41719, 2

82219, 2

136327, 6

229639, 2

347143, 2

380299, 6

528043, 2

654727, 2

> i := 2:
for R from 0 to 30 do
if isprime(poly||i(R)) then print(poly||i(R),
(poly||i(R) - 1)/order(P[1,3](poly||i(R)), poly||i(R))) fi od;

1867, 2

4999, 2

9643, 6

32647, 2

69259, 2

183307, 6

233419, 2

319927, 2

385159, 2

456439, 2

574699, 2

661099, 2

> i := 3:
for R from 0 to 30 do
if isprime(poly||i(R)) then print(poly||i(R),
(poly||i(R) - 1)/order(P[1,3](poly||i(R)), poly||i(R))) fi od;

7477, 1

15361, 320

26053, 1

121633, 2

149173, 1

212677, 1

248641, 40

762721, 6

899233, 38

1046977, 4

1289653, 1

> i := 4:
for R from 0 to 30 do
if isprime(poly||i(R)) then print(poly||i(R),
(poly||i(R) - 1)/order(P[1,3](poly||i(R)), poly||i(R))) fi od;

673, 8

4021, 3

10177, 2

19141, 1

83077, 1

131893, 1

303073, 2

345733, 1

660661, 1

722977, 16

1155841, 2

1237813, 3

1322593, 6

> i := 5:
for R from 0 to 30 do
if isprime(poly||i(R)) then print(poly||i(R),
(poly||i(R) - 1)/order(P[1,3](poly||i(R)), poly||i(R))) fi od;

55711, 6

79147, 2

174079, 38

305947, 18

474751, 2

838171, 2

1012267, 2

1202779, 6

> i := 6:
for R from 0 to 30 do
if isprime(poly||i(R)) then print(poly||i(R),
(poly||i(R) - 1)/order(P[1,3](poly||i(R)), poly||i(R))) fi od;

1279, 18

6571, 10

158527, 2

238879, 6

511579, 6

724447, 2

803611, 2

1260991, 2

1700767, 6

>

Procedure to calculate the Jacobi binomial coefficients mod p :

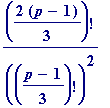(2*(p-1)/3)!/(((p-1)/3)!^2) (mod p ) for prime p with p = 1 (mod 3)

> J_bin := proc(p) local r1, k, r2;
r1 := 1;
for k from 2 to (p-1)/3 do
r1 := r1*k mod p od;
r2 := (p+2)/3;
for k from (p+5)/3 to 2*(p-1)/3 do
r2 := r2*k mod p od;
r2/r1 mod p; end:

J_bin_la := proc(p) mods(J_bin(p), p) end:

>

> p := 3889: J_bin_la(p);

2

> L := [109, 433, 3889, 18253, 21169, 43201, 47629, 73009, 84673, 139969];

L := [109, 433, 3889, 18253, 21169, 43201, 47629, 7...

> for p in L do [p, J_bin_la(p)] od;

[109, 2]

[433, 2]

[3889, 2]

[18253, 2]

[21169, 2]

[43201, 2]

[47629, 2]

[73009, 2]

[84673, 2]

[139969, 2]

>